World's Hardest 'Easy Geometry' Problem
Here are the
World's Hardest Easy Geometry Problem,
as found on Keith Enevoldsen's Think Zone web page:
Solutions to both of these problems can be found far below -- so be careful
how far you scroll below if you don't want to see the answer.
What makes these geometry problems so interesting (and 'hard') is that only
elementary geometry is allowed (no trigonometry). Like, basic rules about
parallel and intersecting lines and the angles formed:
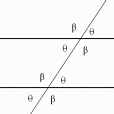
as well as simple
triangle facts:
- the sum of interior angles of a triangle add up to 180°
- isosceles triangle theorem about two equal angles/sides
- an equilateral triangle has three 60° angles and three equal length sides
as well as
what makes two triangles congruent:
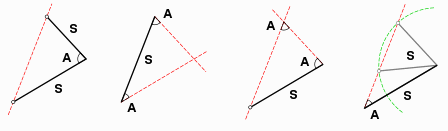
The solutions below are by design not rigorous proofs,
but rather provide just enough information to make the true
solution very obvious to most readers.
You must click to find the images associated with these solutions -- so as to
not spoil the fun for those that want to try to find the solution for themselves
first.
Problem One Solution
Solution One Image
1. Calculate some known angles:
 ACB = 180-(10+70)-(60+20) = 20° ACB = 180-(10+70)-(60+20) = 20°
 AEB = 180-70-(60+20) = 30° AEB = 180-70-(60+20) = 30°
2. Draw a line from point D parallel to
AB,
labeling the intersection with
BC as a new point F and conclude:
 DCF DCF  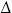 ACB ACB
 CFD = CFD =  CBA = 60+20 = 80° CBA = 60+20 = 80°
 DFB = 180-80 = 100° DFB = 180-80 = 100°
 CDF = CDF =  CAB = 70+10 = 80° CAB = 70+10 = 80°
 ADF = 180-80 = 100° ADF = 180-80 = 100°
 BDF = 180-100-20 = 60° BDF = 180-100-20 = 60°
3. Draw a line FA
labeling the intersection with DB
as a new point G and conclude:
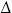 ADF ADF 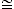 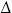 BFD BFD
 AFD = AFD =  BDF = 60° BDF = 60°
 DGF = 180-60-60 = 60° = DGF = 180-60-60 = 60° =  AGB AGB
 GAB = 180-60-60 = 60° GAB = 180-60-60 = 60°
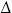 DFG (with all angles 60°) is equilateral DFG (with all angles 60°) is equilateral
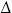 AGB (with all angles 60°) is equilateral AGB (with all angles 60°) is equilateral
4. 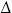 CFA with two 20° angles
is isosceles, so
FC = FA CFA with two 20° angles
is isosceles, so
FC = FA
5. Draw a line CG,
which bisects  ACB and conclude: ACB and conclude:
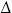 ACG ACG 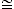 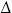 CAE CAE
- FC-CE
= FA-AG
= FE
= FG
- FG
= FD, so
FE
= FD
6. With two equal sides, 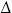 DFE is isosceles and conclude: DFE is isosceles and conclude:
-
 DEF = 30+x = (180-80)/2 = 50 DEF = 30+x = (180-80)/2 = 50
Answer: x = 20°
Problem Two Solution
Solution Two Image
1. Calculate some known angles:
 ACB = 180-(20+60)-(50+30) = 20° ACB = 180-(20+60)-(50+30) = 20°
 AEB = 180-60-(50+30) = 40° AEB = 180-60-(50+30) = 40°
2. Draw a line from point E parallel to
AB,
labeling the intersection with
AC as a new point F
and conclude:
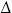 FCE FCE 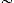 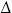 ACB ACB
 CEF = CEF =  CBA = 50+30 = 80° CBA = 50+30 = 80°
 FEB = 180-80 = 100° FEB = 180-80 = 100°
 AEF = 100-40 = 60° AEF = 100-40 = 60°
 CFE = CFE =  CAB = 60+20 = 80° CAB = 60+20 = 80°
 EFA = 180-80 = 100° EFA = 180-80 = 100°
3. Draw a line FB
labeling the intersection with AE
as a new point G and conclude:
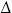 AFE AFE 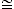 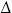 BEF BEF
 AFB = AFB =  BEA = 40° BEA = 40°
 BFE = BFE =  AEF = 60° AEF = 60°
 FGE = 180-60-60 = 60° = FGE = 180-60-60 = 60° =  AGB. AGB.
 ABG = 180-60-60 = 60° ABG = 180-60-60 = 60°
4. Draw a line DG.
Since
AD=AB
(leg of isosceles) and
AG=AB
(leg of equilateral), conclude:
- AD = AG.
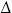 DAG is isosceles DAG is isosceles
 ADG = ADG =  AGD = (180-20)/2 = 80° AGD = (180-20)/2 = 80°
5. Since  DGF = 180-80-60 = 40°, conclude: DGF = 180-80-60 = 40°, conclude:
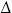 FDG (with two 40° angles) is isosceles, so
DF = DG FDG (with two 40° angles) is isosceles, so
DF = DG
6. With
EF = EG
(legs of equilateral) and
DE = DE
(same line segment)
conclude:
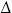 DEF DEF 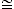 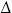 DEG by side-side-side rule DEG by side-side-side rule
 DEF = DEF =  DEG = x DEG = x
 FEG = 60 = x+x FEG = 60 = x+x
Answer: x = 30°
Copyright © 2000-2025 Duckware
|
|