The TED-Ed Frog Riddle is WRONG
duckware.com/tedfrog - January 17, 2017 - Blog Index
|
1. The TED-Ed Frog Riddle
|
|
The Riddle:
As per the TED-Ed "Can you solve the frog riddle?" video
(or visit
ed.ted.com for the full lesson):
"So you're stranded in a huge rainforest and you've eaten a poisonous mushroom. To save
your life, you need the antidote excreted by a certain species of frog. Unfortunately, only the female of the
species produces the antidote. And to make matters worse, the male and female occur in equal numbers and
look identical with no way for you to tell them apart, except that the male has a distinctive croak. And it
may just be your lucky day. To your left, you've spotted a frog on a tree stump. But before you start running
to it, you're startled by the croak of a male frog coming from a clearing in the opposite direction. There
you see two frogs, but you can't tell which one made the sound. You feel yourself starting to lose
consciousness and realize you only have time to go in one direction before you collapse. What are your
chances of survival if you head for the clearing and lick both of the frogs there? What about if you go
to the tree stump? Which way should you go?"

Run to the clearing or run to the stump (or die trying to solve this riddle)?
|
The controversy: Presh Talwalkar published a
"TED-Ed's Frog Riddle Is Wrong" video
on his "Mind Your Decisions" YouTube channel slamming a TED-Ed video for
being incorrect, and presented his method of finding the 'correct' probability of a female frog
in the clearing. The only problem is that Presh assumed female croaking to 'prove' TED-Ed wrong.
|
2. The wrong answer to the riddle
|
|
TED-Ed answer: TED-Ed states that the probability is 2/3 for finding a female frog in the clearing and
1/2 for finding a female frog on the tree stump, citing conditional probability.
That is the wrong answer.
A horrible conditional probability example:
This TED-Ed riddle is a horrible example of conditional probability because it leaves many
critical assumptions open to interpretation. What about biology and the fact that a male frog
croaks to attact a female frog? Apparently we must ignore that. Does the female frog croak at all?
Not in real life! So, keep as much as possible a variable and solve. So, just state that male frogs croak with a
probability of 'p' and females croak with the probability of 'q' and solve for that (you can always
set q=0 after the fact)!
It appears very clear that TED-Ed intended for the distinctive croak of a male frog from
the clearing to simply (only) inform us that there is a male frog in the clearing.
However, what TED-Ed did not plan for is that it also tells us that
there is no croaking male on the tree stump!
So it matters HOW you learned that there was a male frog in the clearing! Did an 'oracle'
tell you there was a male frog in the clearing (does not affect tree stump). Or did you hear
only a croak coming from the clearing (also affects the tree stump)? It matters.
See 'oracle mode' in simulation far below.
Also, the
"Dig Deeper"
lesson section for the frog riddle on the TED-Ed site points to the
Monty Hall problem
(more info from wiki),
which confirms further that TED-Ed intended to present the 'oracle' problem.
Monty Hall problem: You are on a game show and there are three boxes. Inside only one
box are the keys to a brand new car! You are asked to select a box.
After your box selection, the game show host reveals an empty box and asks if you would like
to stick with your original selection, or switch to the one remaining box. What should you do?
For most people, the answer -- that switching results in a 2/3 chance to win the car -- appears impossible.
But a little thought makes it obvious.
For the 1/3 of the time that you initially picked the box with the car keys, the host
reveals one losing box, you switch to the one other losing box, and you lose. But
for the 2/3 of the time that you initially picked a losing box, the host reveals the other
losing box, you switch to the box with the car keys, and you win!
Distinctive croak: The fact that you learned about the male frog in the clearing
pair by hearing a distinctive croak of a male, and that there were no other croaks,
not only changes the outcome space for the clearing, but also changes the outcome space
for the tree stump (as there were no croaks from there)! Also, the actual probability value of
a male frog croaking (or not) plays a key role in the probability is of finding a female frog.
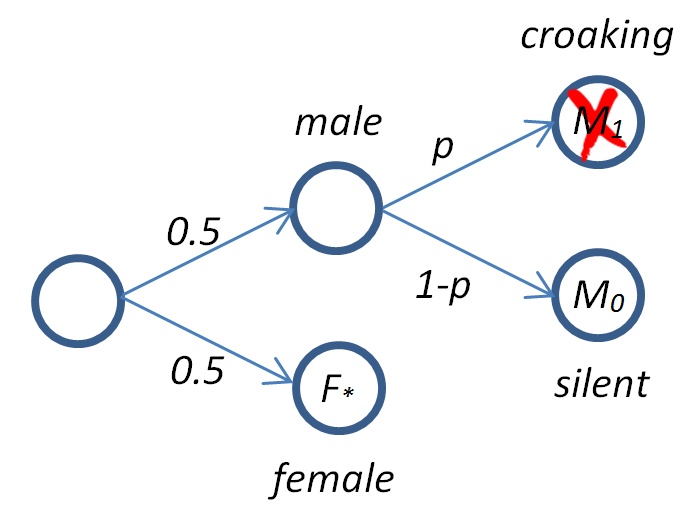
Croak probability matters!
|
To clearly 'see' that the probability of a male frog croaking matters a LOT, consider
what happens when the probability of a male croaking is 100%.
Then any 'silent' frog MUST be a female frog! And the fact that you heard a single male
distinctive croak coming from the clearing means that the other two (silent) frogs
(one in clearing; one on tree stump) MUST both be female frogs!
The hilarious TED-Ed response: I actually filled out the TED-Ed contact form and
reported a problem with the math in the video (case #721930).
The response from TED-Ed was from support, and because that person was not a mathematician,
I will not quote that person directly, but they defended the frog video, effectively stating
'on the stump there is no male croak, but likewise, there is also no female croak,
so that means 1/2 is the right answer'.
|
3. The correct answer to the riddle
|
|
Please refer to the next sections for a justification of these answers
Q: "What are your chances of survival if you head for the clearing and lick both of the frogs there?"
Answer: The probability of finding a female frog in the clearing, given that you heard
a distinctive male croak coming from the clearing (and no other croaks),
is (1-q)/(2-p-q), where 'p' is the probability of a male
frog croaking and 'q' is the probability of a female frog croaking.
With p=0.5 and q=0, the probability is 2/3.
Q: What about if you go to the tree stump?
Answer: The probability of finding a female frog on the tree stump, given that you heard
a distinctive male croak coming from the clearing (and no other croaks),
is (1-q)/(2-p-q), where 'p' is the probability of a male
croaking, and 'q' is the probability of a female frog croaking.
With p=0.5 and q=0, the probability is 2/3.
Q: Which way should you go?
Answer: No matter what the probability of a male frog croaking or female frog croaking is,
both ways result in the same probability of finding a female frog!
But, given that you about to "lose consciousness"
and "collapse", it is better to not waste time -- and therefore, you should lick just ONE frog, not two, so...
Your best option is go to to the tree stump!
|
4. Background: Conditional Probability
|
|
The TED-Ed riddle is a classic conditional probability situation. Namely, what is the probability
of an event A ('finding a female frog in the clearing / on the stump'), given
that a condition B has occurred
("you're startled by the croak of a male frog coming from a clearing in the opposite direction").
Conditional probability formula: The solution is the conditional probability
formula (seen right). This formula means: The probability of A given B equals the
probability of A and B happening together, divided by the probability of just B.
Another way of thinking about conditional probability is that it in effect creates a
new sample space 'B', which is a subset of the original sample space -- and then
what is the probability of 'A' happening within that new sample space 'B'.
An Example: Roll two fair dice. The sample space is 6×6=36 (equally likely) items.
What is the probability only one of the rolls was a 5?
We inspect the sample space and find 10 matches. So the answer is 10/36, or just under 28%.
Now, what is the probability only one of the rolls was a 5, if the sum of both dice equals 9?
P(B) is P(if the sum of both dice equals 9), and P(A) is P(what is the probability only one of the rolls was a 5).
Solving, we get a P(B) of 4/36, and a P(A∩B) of 2/36 for a final answer is then (2/36)/(4/36), or 50%.
The key to understanding the different answer is realizing that the condition creates a new sample space.
Something similar is happening with the frog riddle. The key to answering the frog riddle
is correctly finding the new sample space 'B'.
Wiki on Conditional Probability.
Conditional probabilities can sometimes be incredibly tricky. You will only get the 'correct' answer
when you (1) properly enumerate (or account for) ALL possible outcomes and (2) properly filter out
non-condition outcomes.
|
5. The math behind the correct answer
|
|
Before we start, let's clarify some items:
P(male or female): We must know the probability of a male vs female frog. The original riddle states
'equal numbers', which we will translate as 'equally likely' -- even though it is not
precisely that (see a later section for a more detailed look at this).
P(male croak): We will use the probability of a male frog croaking of 'p' -- keeping it
a variable! This way, after the fact, you can set 'p' to anything.
P(female croak): We will use the probability of a female frog croaking of 'q' --
keeping it a variable! This way, after the fact, you can set 'q' to anything -- including
zero, which eliminates female croaking.
one and only one male croak: The original TED-Ed video makes it clear in its subsequent narration that
"startled by the croak of a male frog" means hearing ONE and only one male
croaking, which eliminates multiple males croaking at the same time.
and no other croaking: The riddle narration makes it clear that you are looking
at the frog on the stump when you are started by a distinctive male croak from the
clearing. So you know there was no croak coming from the stump. As for the clearing,
the riddle says "which one made the sound", which means a single sound was heard.
| New Sample Space (highlighted) |
F0 — F0F0
F0 — F0F1
F0 — F1F0
F0 — F1F1
F0 — F0M0
F0 — F0M1
F0 — F1M0
F0 — F1M1
F0 — M0F0
F0 — M0F1
F0 — M1F0
F0 — M1F1
F0 — M0M0
F0 — M0M1
F0 — M1M0
F0 — M1M1
|
|
F1 — F0F0
F1 — F0F1
F1 — F1F0
F1 — F1F1
F1 — F0M0
F1 — F0M1
F1 — F1M0
F1 — F1M1
F1 — M0F0
F1 — M0F1
F1 — M1F0
F1 — M1F1
F1 — M0M0
F1 — M0M1
F1 — M1M0
F1 — M1M1
|
|
M0 — F0F0
M0 — F0F1
M0 — F1F0
M0 — F1F1
M0 — F0M0
M0 — F0M1
M0 — F1M0
M0 — F1M1
M0 — M0F0
M0 — M0F1
M0 — M1F0
M0 — M1F1
M0 — M0M0
M0 — M0M1
M0 — M1M0
M0 — M1M1
|
|
M1 — F0F0
M1 — F0F1
M1 — F1F0
M1 — F1F1
M1 — F0M0
M1 — F0M1
M1 — F1M0
M1 — F1M1
M1 — M0F0
M1 — M0F1
M1 — M1F0
M1 — M1F1
M1 — M0M0
M1 — M0M1
M1 — M1M0
M1 — M1M1
|
|
| 'heard a male croak in clearing' reduces 64 items to 8 |
Conditional Probability: This riddle is a classic conditional probability
problem (formula given in section above). Given the 'condition'
"you're startled by the croak of a male frog coming from a clearing in the opposite direction",
what is
(1) the probability of a female frog at the stump, and
(2) the probability of a female frog in the clearing?
Setup: Start by enumerating ALL possible outcomes of seeing one frog
on a stump and two frogs in the clearing (F=female, M=male), where the
subscript of each frog F/M states if that frog is croaking (1=yes, 0=no).
The result (seen right) is (2×2) × (2×2×2×2)
= 4×16 (4 cols; 16 rows) = 64 items.
Format: Each item is "(stump frog) — (clearing frog pair)".
Notice that each column is one stump frog option, and
the 16 'frog pair' entries within all columns are identical.
The probability of an item, given 'M' males of which 'm' are croaking, and 'F' females of which 'f' are
croaking is:
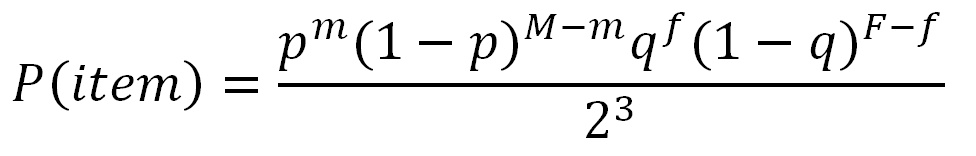
When p=0.5 and q=0.5 this greatly simplifies to just (1/2)^6, or 1/64.
P(B)=P(heard a male croak in clearing and no other croaks):
Look through all 64 items for a single male croak coming from the clearing
frog pair and NO other croaks.
On matches, mark/highlight the entire item with a yellow highlight.
These items are the new sample space.
The sum of all 8 marked/yellow P(item) probabilities for any 'p' and 'q' is:
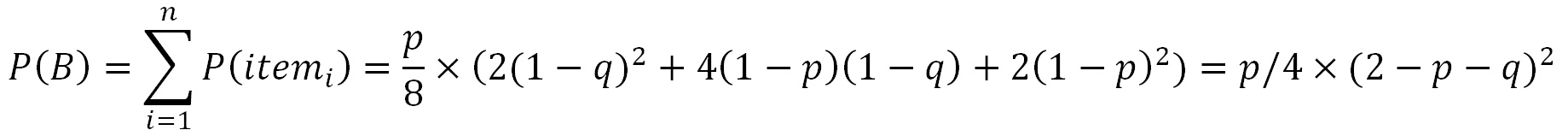
P(female on stump|B):
For all items within P(B), if there is a female 'at the stump', color that female red.
The sum of all 4 red P(item) probabilities for any 'p' and 'q', is:
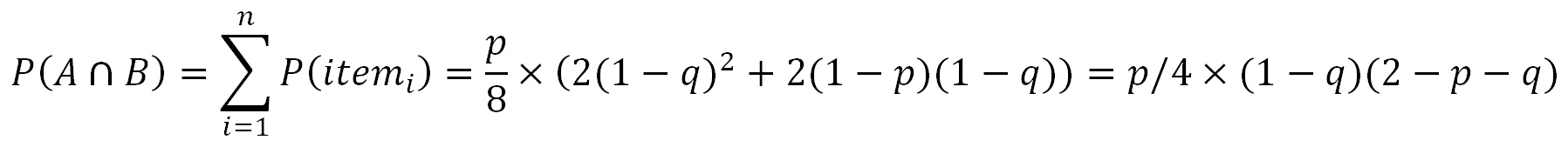
So the answer for P(female on stump|B) is:
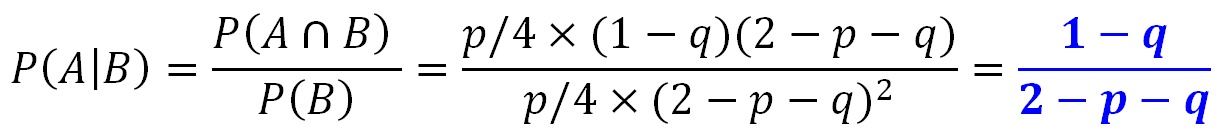
P(female in clearing|B):
For all items within P(B), if there is a female 'in the clearing pair', color that female blue.
The sum of all 4 blue P(item) probabilities for any 'p' and 'q', is:
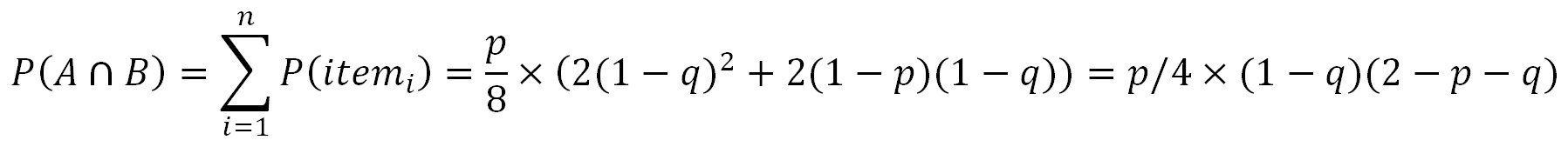
So the answer for P(female in clearing|B) is:
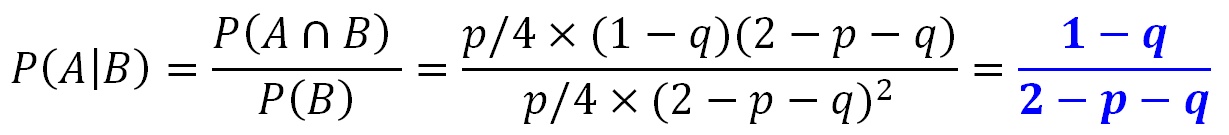
Indistinctive female croaking? One possible interpretation of the riddle narration is
that when the distinctive male croak is heard, that there can be 'indistinctive'
female croaking going on as the same time. In a prior version of this paper, I calculated
that possibility and the formula result is exactly the same as setting 'q' to zero.
So ignoring female croaking (no impact a hearing the 'distinctive' male croak) is exactly
the same as no female croaking. That makes sense. But then where do you do this?
Only in the clearing formula? In the tree stump formula? Both? What a mess.
How TED-Ed messed up: As it is impossible to know exactly what TED-Ed
intended to do with this riddle, but let's assume that TED-Ed knew what they
were (mostly) doing. Based upon everything they did, and some common sense,
the most logical conclusion is that TED-Ed used p=0.5, q=0, messed up creating
the sample spaces, got lucky in the clearing (correct answer but wrong math),
and just flat out messed up on the tree stump (wrong answer and wrong math):

Tree stump probability tree
|
Tree Stump: For the tree stump, there is only one frog with possibilities (M,F).
When you extend that to only one male frog croaking in the clearing and no
female croaking, you get either (1) a female, or (2) a non-croaking male -- or a sample space
of (F*, M0). Also, refer to the probability tree seen right.
Therefore, the conditional probability of finding a female frog at the tree stump, given
a male croak only from the clearing (and p=0.5, q=0) is (1/2)/(1/2+1/4), or 2/3. But TED-Ed used a sample
space of (M,F), and calculated 1/2, the wrong answer!
The key mistake that TED-Ed made is not understanding that the probability of a male
frog croaking affects both the clearing and the tree stump -- and simply (wrongly)
presumed that F* and M0 are both equally likely.
The only way to get the 1/2 TED-Ed answer is if male frogs never croak (p=0)!
Clearing: For the clearing, there are two frogs with possibilities (FM,MF,MM).
When you extend that to only one male frog croaking and no female croaking, you get
(F*M1, M1F*, M1M0, M0M1).
Therefore, the conditional probability of finding a female frog in the clearing, given
a male croak only from the clearing (and p=0.5, q=0) is (1/8+1/8)/(1/8+1/8+1/16+1/16) = 2/3.
But TED-Ed used a sample space of (FM,MF,MM), calculated 2/3, and got lucky getting
the correct answer using the wrong math.
|
7. Presh Talwalkar answered the wrong question
|
|
The wrong question:
Presh Talwalkar focused on the wrong question. He focused on the probability of a female frog
in the clearing, stating that it was 1/2 and not the 2/3 that TED-Ed calculated.
But the only way to get that result was to assume that female frogs croak with
probability of 0.5 (but female frogs don't croak in the real world).
That was a mistake and the wrong tactic to take.
Presh should have instead just calculated the probabilities either way and shown that
they are equal!
A mess of contradictory information: PT's blog and YouTube video are a mess of contradictory
information. The blog states "If we assume only male frogs croak" and his YouTube video contradicts
that stating "we're going to assume that (male and female frogs croaking) are all equally likely events".
|
8. But female frogs don't croak!
|
|
Correct! The reason the formulas were created was not to get a specific answer, but to
clearly show that it does not matter what the croaking probabilities are -- the probability
of a female in the clearing is exactly the same as the probability of a female on the stump.
To eliminate female frog croaking, just set q=0 in the formulas.
|
9. Can you solve these riddle variations?
|
|
Take the TED-Ed riddle presented at the top of this page. The probability of a
male croaking is 0.5. Females don't croak. Given these ground rules, can you
solve these other riddles/questions...
Riddle One: Take the TED-Ed riddle, and reword it after "To your left"...
You see one frog jump onto the stump.
You see a second frog jump onto the stump, and recognize it as a 'tagged' male.
You see a third frog jump onto the stump. All three frogs look identical.
You only have time to lick ONE frog.
Which frog are you going to lick (the first or the third), and why?
Isn't it amazing that mathematicians that find fault with the TED-Ed riddle incorrectly
translate "the male and female occur in equal numbers" to "equally likely". Both are very close
to each other, but not the same thing! "Equal numbers" means that you start out
with 'N' male frogs and 'N' female frogs!
With N female frogs and N male frogs, there is a N/(2N) = 1/2 probability that
the first frog is a female. The second frog is known to be a male.
So what about the third frog? Do the math and there is a 1/(2-1/N) probability that the third frog is
a female, giving an ever so slight advantage to the third frog being a female! As N goes to
infinity, 1/(2-1/N) becomes the expected 1/2 in the case of "equally likely".
TIP: A spreadsheet is your best friend. My steps: (1) create a working model in a spreadsheet,
(2) derive the formula on paper, and (3) enter the formula into the spreadsheet and confirm that it
and the model produce the same results for varied 'N'.
So the answer is: You should lick the third frog.
Riddle Two: (1) What is the probability you will hear a single male croak
from a female/male pair? (2) What is the probability you will hear a single croak from a male/male
pair? (3) What is the probability you will hear croak(s) from a male/male pair?
First answer is 1/2 (the only probability fork when a female does not croak is for the male croaking, or not)
Second answer is also 1/2. (because you are excluding when they both don't
croak or when they both do croak). Third answer is 3/4 (1/4 is when they both don't croak).
The single croak two frog paradox: Given the probability of a frog croaking is 0.5, what is the
probability of hearing a single croak from (1) ONE frog, (2) TWO frogs.
Surprisingly, the same! For one frog, it is obviously 1/2.
For two frogs, it is 2/4 (01,10) of (00, 01, 10, 11), or the same 1/2. The key is realizing that with
two frogs, one frog is croaking and the other frog MUST not croak!
|
10. ALWAYS run a Q+D simulation -- to verify your math, and the riddle
|
|
Validate the results: Run a simulation and verify that the calculated math answer
matches the simulation answer.
Even the smallest wrong assumption in reading a probability problem can
dramatically impact results.
I always write a quick and dirty Monte Carlo Simulation to 'confirm' (or refute)
calculated math results. In a matter of minutes (of coding), the simulation will reveal the
true 'real-world' measured probability of the event (or riddle) in seconds!
▶Run the frog simulation - confirms that
the answer is the same both ways
Warning: There is a danger that you make a wrong assumption and then code that wrong
assumption into the simulation, which only further confirms your wrong assumption.
If the simulation confirms your math calculations, your math calculation may be correct.
But if the simulation refutes your math calculations, then you absolutely KNOW you have
a problem (either in the math, or in the simulation).
Another example: PT describes a 'Boy or Girl Paradox' in his video.
This simulation
shows how easy it is to confirm those results with a simulation.
Simulations work!
|
|